
`` experience proves that anyone who has studied geometry is infinitely quicker to grasp difficult
subjects than one who has not.''
Plato - The Republic, Book 7, 375 B.C.
Below are some interesting objects sitting on a chess board. (The battery is mine, object 1 is my little daughter's & object 2 was borrowed from my warlike son.) The question we are investigating is 'what are the respective distances of those 3 objects from the camera that took the picture?', and the parallel with the Hughes movie frame in question is obvious. In this case, however, I happen to know the answer in advance, because I took the photo myself. The camera was in fact in line with the very edge of the chess board. And, because the objects are on a chess board, we can immediately see which object is furthest away and also make a good guess at their respective distances - which, of course, is why I put them on a chess board in the first place.

The eesential point to notice is that as the distance of the object from the camera increases, so the level at which the base of the object meets the chess board moves higher up the picture. Thus the base of the pink cup is higher up the picture than the base of the soldier, which is higher than the base of the battery. There is an exact mathematical relationship between these heights (in the picture) and the object distances from the camera (in reality). The relationship is derived below. For those who don't wish to be bombarded with mathematics, the result can be taken on trust and you can continue to see the results of the analysis (as applied to the Hughes frame) here.

(Above) In this case, the distances marked with the green arrows are inversely proportional to the distances of the respective vehicles from Hughes.
The procedure we will follow is this : 1) Find the viewer's horizon 2) find the points in the photo where the objects meet the board 3) measure the distance, in pixels, vertically down the photo from the horizon to that point. Then the distance of each object from the viewer will be inversely proportional to that distance. For eg, the distance 'viewer -> object 2' will be proportional to 1/ d2 (see illustration above ) . The distance 'viewer-object 1' will be proportional to 1/ d1, etc etc. The diagram below illustrates why this is so.
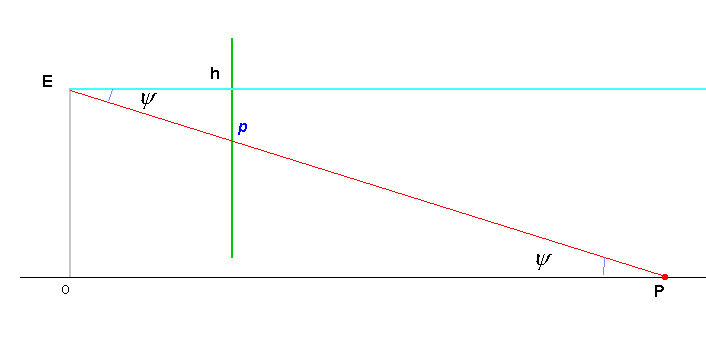
In the diagram above, ' E ' represents the photographer's eye, the green vertical the picture plane, OP the ground - assumed flat & horizontal * , ' h ' the horizon in the picture plane, ' P ' a location on the ground, ' p ' the image of that point in the picture plane.
By simple geometry, since triangles Ehp & EOP are similar, then
hp / Eh = EO / OP = tan (![]() );
);
Thus
hp X OP = Eh X EO = a constant for this particular picture.
(Effectively the focal length of the camera multiplied by the height of the camera above the plane in question.)
This means that for ALL points P on the plane, the product of the distance hp with the distance OP is the same.
|
Thus we have the crucial result : the distance OP & the distance hp are inversely proportional. |
All that is neccessary to work out all such camera- object distances, then, is to find this invariant : Eh X EO.
The argument actually extends ( essentially unchanged) very simply to cases where
the picture plane is not at right angles to the ground / base plane.
Thus the essential point : In a suitable photograph, the distance of the image of an object down from the horizon, measured on the photograph itself, is inversely proportional to the distance of that object from the photographer in reality.
The horizon is easily found by producing the convergent parallels (blue lines) until they meet. The point at which they meet is on the original viewer's horizon. The horizon is then drawn as a red line running - horizontally - across the picture through that point. ( h to h). We then measure down the picture, in any convenient units, to the bases of the objects. We get d1= 96 (pixels), d2=108 , d3 = 151. Then we immediately know that the distance of the original viewer from object i is equal to k / d(i) for some constant k, which (crucially) is the same constant for all points on the surface of the board in this picture.
Now, we simply need to find that constant of proportionality and we will be in a a position to find all such distances in the chess board photo. Now, we happen to know that the photo was taken from the edge of the board. So for object 1, it's actual distance from the camera would be ' 7 squares ' (to it's nearest point. We will measure distance in terms of the length of the side of one of those squares on the board) . So now we can find ' k', since :
distance (i) = k / d(i)
In this case, this boils down to ..
7 = k / d1
d1= 96, so ..
7 = k / 96
So k= 7 X 96 = 672
Let's see how that works out for the other two objects :
distance (2) = k / d2 = 672 / 108 = 6.22.
distance (3) = k / d3 = 672 / 151 = 4.45
A glance at the photo will show that these measures are accurate - noting that the 3.5 chess board squares nearest the camera do not appear in the photo. Thus the theory really does work in practice.
"Mapping from a single photograph [is] only useful for plane (2D) objects. Obliquely photographed plane objects show perspective deformations which have to be rectified. For rectification exists a broad range of techniques. Some of them are very simple. However, there are some limitations. To get good results even with the simple techniques, the object should be plane (as for example a wall), and since only a single photograph is used, the mappings can only be done in 2D "
(Intro To Photogrammetry at: http://www.univie.ac.at/Luftbildarchiv/wgv/intro.htm)
To the extent that Houston Street is 'plane', and to the extent that Hughes camera lens was free of radial and decentering distortion [1] we should expect the result to accurately mirror reality.
We are now ready to apply this knowledge to the analysis of the Hughes frame. Click here to continue.
[1] ""..practical lens systems are nonlinear and can easily introduce significant distortions in the intrinsic perspective mapping from external optical rays to internal pixel coordinates. This sort of distortion can be corrected by a nonlinear deformation of the image-plane coordinates... to correct for distortion, all we need to do is to observe straight lines in the world and deform the image to make their images straight. "
http://www.inrialpes.fr/movi/people/Triggs/isprs96/node10.html
The relevant frames from the Hughes movie, being full of Houston St, architecture, contain many images of straight lines. No noticeable curvature is present in any of these images. Thus the camera system was effectively free of distortion. A more thorough study could be undertaken with the actual film, or with a good copy.